数据结构总结

发布于 10 天前  96 次阅读

最近一直很忙，从接大活到准备实习面试到速通期末，一直没有时间发博客，发个复习期末写的数据结构水一篇:)



test.md




逻辑结构和存储结构

  • 逻辑结构：
    • 1.线性：线性表，栈，队列，双队列，数组，串
    • 2.非线性：二维数组，多维数组，广义表，树
  • 存储结构：顺序存储（顺序表，顺序队列），链式存储（链表，链队列）
  • 计算第i个元素存储位置：l(ai)=l(a1)+(i-1)*l
  • 行序二维数组的存储位置计算：l(A[i][j])=l(A)+(i⋅n+j)⋅l

顺序表

// 初始化
void InitList(SqList* l){
    for(int i = 0 ; i < MAXSIZE ; i++){
        l->data[i] = 0;
    }
    l -> length = 0;
}

// 打印
void print(SqList L)
{
    int i = 0;
    for (i = 0;i < L.length;i++)
        printf("%d ", L.data[i]);
    printf("\n");
}

// 插入
Status Insert(SqList* l,int i,EleType data){
    if(l->length + 1 < i || i<1 ){
        return ERROR;
    }

    for(int j = l->length ; j >= i-1 ; j--){
        l -> data[j] = l -> data[j-1];
    }
    l -> data[i-1] = data;
    l -> length++;
    return OK;
}

链表

  • 尾插要考虑2种：
    • 如果链表为空，则直接插入即可。
    • 如果链表不为空，则需要找到尾结点再插入。
  • 尾删要考虑3种：
    • 链表为空。
    • 链表中只有一个结点。
    • 链表中有一个以上结点。
#include <stdio.h>
#include <assert.h>
#include <stdlib.h>

typedef struct Node
{
    int data;
    struct Node* next;
}Node;

// 创建新节点
Node* BuyNode(int data){
    Node* newnode = (Node*)malloc(sizeof(Node));
    newnode -> next = NULL;
    newnode -> data = data;
    return newnode;
}
// 遍历打印
void printList(Node* head){
    Node* cur = head;
    while (cur)
    {
        printf("%d-> ",cur -> data);
        cur = cur -> next;
    }
    printf("^\n");
}

// 尾插
void insertRear(Node** head,int data){
    Node* newnode = BuyNode(data);
    if(!*head){
        *head = newnode;
    }else{
        Node* cur = *head;
        while (cur -> next)
        {
            cur = cur -> next;
        }
        cur -> next = newnode;

    }
}

// 头插
void insertHead(Node** head,Node* CurrentHead,int data){
    Node* newnode = BuyNode(data);
    if(!*head){
        *head = newnode;
    }else{
        newnode -> next = CurrentHead;
        *head = newnode;
    }
}

// 插入
void insert(Node** head,Node* pos,int data){
    Node* newnode= BuyNode(data);
    if(*head == pos){
        newnode -> next = *head;
        *head = newnode;
    }else{
        Node* cur = *head;
        while (cur->next != pos)
        {
            cur = cur -> next;
        }
        cur -> next = newnode;
        newnode -> next = pos;

    }
}

// 删除
void Delete(Node** head,Node* pos){
    if(*head = pos){
        *head = (*head) -> next;
    }else{
        Node* cur = *head;
        while (cur -> next != pos)
        {
            cur = cur->next;
        }
        cur -> next = pos -> next;
        free(pos);
        pos=NULL;
    }
}

// 查找
Node* find(Node* head, int i)
{
    while (head)
    {
        if (head->data == i)
        {
            return head;
        }
        head = head->next;
    }
    return NULL;
}

int main(){
    Node* head = NULL;
    insertHead(&head,head,12);
    insertHead(&head,head,33);
    insertHead(&head,head,4);
    insert(&head,find(head,33),97);
    printList(head);
    return 0;
}

循环链表

终端节点->next = 头节点。
判断是否为空：空循环链表的头节点->next=头节点（头节点->next->next->next都=头节点），
循环条件：cur->next != head

队列

循环队列

  • 运算：
    • 长度：(rear - front + MAXSIZE) % MAXSIZE
    • 判空：rear == front
    • 判满：(rear + 1) % MAXSIZE == front
    • 入队：rear = (rear + 1) % MAXSIZE
    • 出队：front = (front + 1) % MAXSIZE
    • 遍历：cur = (cur + 1) % MAXSIZE

在这个例子中，rear指向的数据始终为空，来区分队空和队满

#include <stdio.h>
#include <stdlib.h>
#define MAXSIZE 4
typedef struct 
{
   int front;
   int rear;
   int data[MAXSIZE];
}Sequece;

// 判满
int isFull(Sequece* Seq){
    if(Seq -> front ==  (Seq ->rear + 1) % MAXSIZE){
        return 1;
    }else{
        return 0;
    }
}

// 判空
int isNull(Sequece* Seq){
    if(Seq -> rear == Seq -> front){
        return 1;
    }else{
        return 0;
    }
}

// 遍历
void displaySequeue(Sequece* Seq) {
    int length = (Seq -> rear - Seq -> front + MAXSIZE) % MAXSIZE;
    printf("队列长度为%d，front = %d，rear = %d: " , length , Seq -> front , Seq -> rear);
    int cur = Seq -> front;
    while (cur != Seq -> rear)
    {
        printf("%d ",Seq -> data[cur]);
        cur = (cur + 1) % MAXSIZE;
    }
    printf("\n");

}

// 初始化
void init(Sequece** Seq){
    *Seq = (Sequece*)malloc(sizeof(Sequece));
    (*Seq) -> front = 0;
    (*Seq) -> rear = 0;
    displaySequeue(*Seq);
}

//入队
void Enter(Sequece* Seq , int data){
    if(isFull(Seq)){
        printf("队列已满无法入队。");
    }else{
        Seq -> data[Seq -> rear] = data;
        Seq -> rear = (Seq -> rear +1) % MAXSIZE;
    }
    displaySequeue(Seq);
}

// 出队
void Delete(Sequece* Seq){
    if(isNull(Seq)){
        printf("队列为空无法出队");
    }else{
        Seq -> front = (Seq -> front + 1) % MAXSIZE;
    }
    displaySequeue(Seq);
}

链队列

// 链式结构：表示队列
typedef struct QListNode
{
    struct QListNode* _next;
    int _data;
}QueueNode;

// 队列的结构
typedef struct Queue
{
    QueueNode* _front;
    QueueNode* _rear;
}Queue;

QueueNode * BuyQueueNode(int x)    
{
    QueueNode * cur = (QueueNode *)malloc(sizeof(QueueNode));
    cur->_data = x;
    cur->_next = NULL;
    return cur;
}

 // 初始化
void QueueInit(Queue* q)
{
    q->_front = NULL;
    q->_rear = NULL;
}

// 入队
void QueuePush(Queue* q, int x)  //队列尾部入数据
{
    QueueNode * cur = BuyQueueNode(x);  //先把创建好的节点传过来
    if (q->_front == NULL)             //若是队列本身为空，队列里就只有这一个节点，又为队列头又为队列尾
    {
        q->_front = q->_rear = cur; 
    }
    else
    {
        q->_rear->_next = cur; //否则，链表尾插操作
        q->_rear = cur;
    }
}
void QueuePop(Queue* q)     //队列头部出数据
{
    if (q->_front == NULL)    //本身队列为空，不做操作
    {
        return;
    }
    QueueNode* tmp = q->_front->_next;   //先保留下一个节点，防止断链
    free(q->_front);
    q->_front = tmp;   //更新队列头部
}

栈

顺序栈

判空：top=-1
入栈：

S->top++;   //栈顶指针增加一
S->data[S->top] = e;

出栈：

S->top--;   //栈顶指针减一

链栈

判空：S->top=NULL
入栈：

// 入p节点
p->data = e;
p->next = S->top;    //把当前的栈顶元素赋值给新节点的直接后继
S->top = p; //将新的结点S赋值给栈顶指针

出栈：

p = S->top; //将栈顶结点赋值给p
S->top = S->top->next;  //使得栈顶指针下移一位，指向后一结点
free(p);

广义表

  • 定义：又称列表，也是一种线性存储结构，既可以存储不可再分的元素，也可以存储广义表，如广义表 LS = {1,{1,2,3}}
  • 原子：如LS的1
  • 子表：如LS的{1,2,3}
  • 长度：原子+子表个数，如 {1,{1,2,3}} 长度为2
  • 深度：括号个数，如 {1,{1,2,3,{1,2}}} 深度为3
  • 表头和表尾：当广义表不是空表时，称第一个数据（原子或子表）为"表头"，剩下的数据构成的新广义表为"表尾"。
    • 除非广义表为空表，否则广义表一定具有表头和表尾，且广义表的表尾一定是一个广义表。
    • 如(a,b)表头：a，表尾：(b)
  • 结构定义
typedef struct GNode {
    int tag;                // 标志域, 0表示原子, 1表示子表
    union {
        int atom;          // 原子结点的值域
        struct GNode* hp;  // 子表结点的指针域, hp指向表头
    } subNode;
    struct GNode* tp;     // 指向下一个数据元素
} GLNode, *Glist;

如('a', ('b', 'c'), 'd'):
image_mak

树

二叉树

  • 满二叉树：每一层都满
  • 完全二叉树：除最后一层都满，最后一层右边可以有缺失
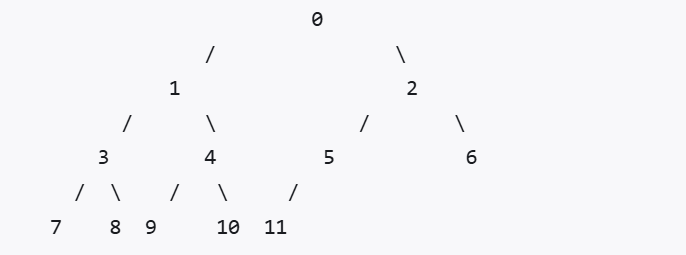
    image_mak

    • 深度=log2(n)+1
#include <stdio.h>
#include <assert.h>
#include <stdlib.h>

// 结构定义
typedef struct binarytreenode
{
    int data;
    struct binarytreenode *Lnode;
    struct binarytreenode *Rnode;
} BiTNode,*BiTree;

// 创建二叉树
void creatTree(BiTree* Tree){
    char c;
    scanf("%c",&c);

    if(c == '#'){
        *Tree = NULL;
    }else{
        *Tree = (BiTNode*)malloc(sizeof(BiTNode));
        (*Tree) -> data = c;
        creatTree(&((*Tree) -> Lnode));
        creatTree(&((*Tree) -> Rnode));
    }
}

// 先序遍历
void pre(BiTree Tree){
    if(!Tree){
        return;
    }
    printf("%c",Tree -> data);
    pre(Tree -> Lnode);
    pre(Tree -> Rnode);
}

// 中序遍历
void mid(BiTree Tree){
    if(!Tree){
        return;
    }
    mid(Tree -> Lnode);
    printf("%c",Tree -> data);
    mid(Tree -> Rnode);
}

// 后序遍历
void after(BiTree Tree){
    if(!Tree){
        return;
    }
    after(Tree -> Lnode);
    after(Tree -> Rnode);
    printf("%c",Tree -> data);
}

线索二叉树

解决叶子节点的左右分支需要消耗空间。

  • 若左子树为空，左指针指向前驱节点

  • 若右子树为空，右指针指向后驱节点

  • ltag==0，指向左孩子；ltag==1，指向前驱结点

  • rtag==0，指向右孩子；rtag==1，指向后继结点
    画图：先写出中序遍历，然后为左右节点为空的补上前驱或后继节点
    先序线索二叉树的遍历：

TBTNode *First(TBTNode *p){
    while(p->ltag == 0) p = p->lchild; //相当于找到树的最左下的结点
    return p;
}

TBTNode *Next(TNTNode *p){
    if(p->rtag == 0){
        return First(p->rchild);
    }
    return p->rchild;      //rtag=1，直接返回后继线索rchild,因为线索化后，rchild就是线索了，指向后继结点
}

void Inorder(TBTNode *root){
    for(TBTNode *p = First(root); p != NULL; p = Next(p))
        Visit(p);   
}
  • 画图
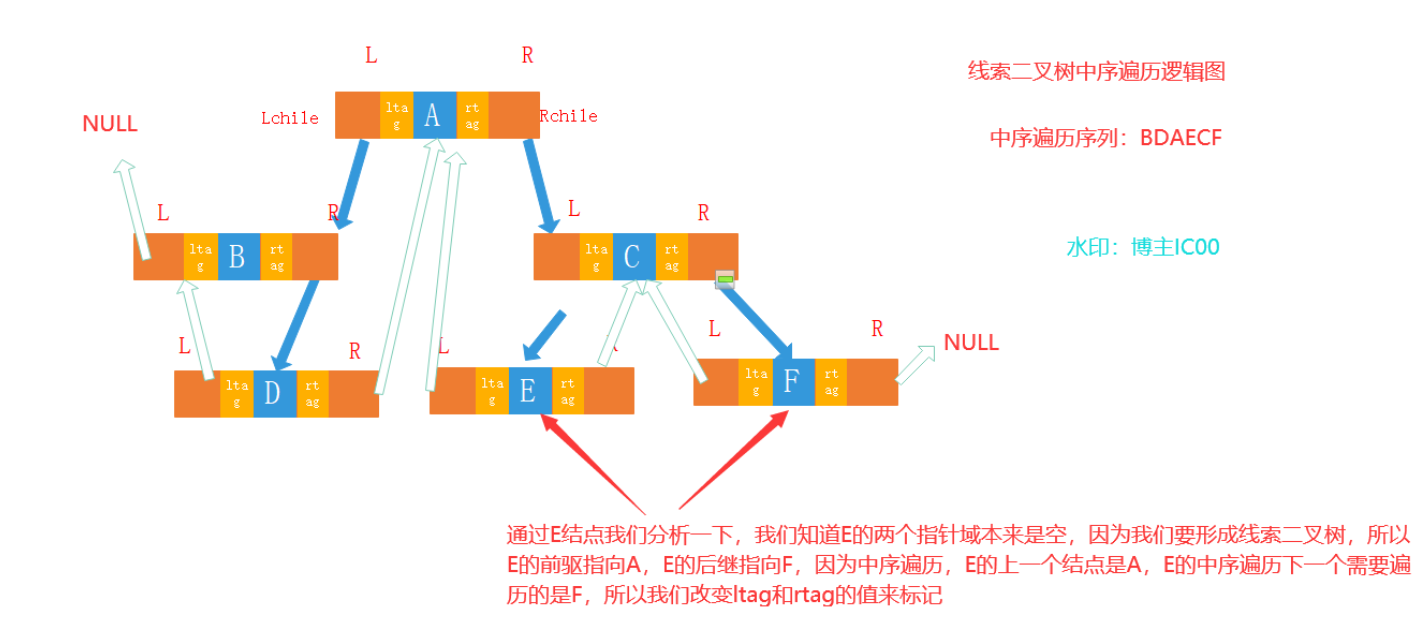
    image_mak

存储结构表示

双亲表示法

  • 用数组表示树
    在每个结点中，附设一个指示器parent指示其双亲结点到链表中的位置。
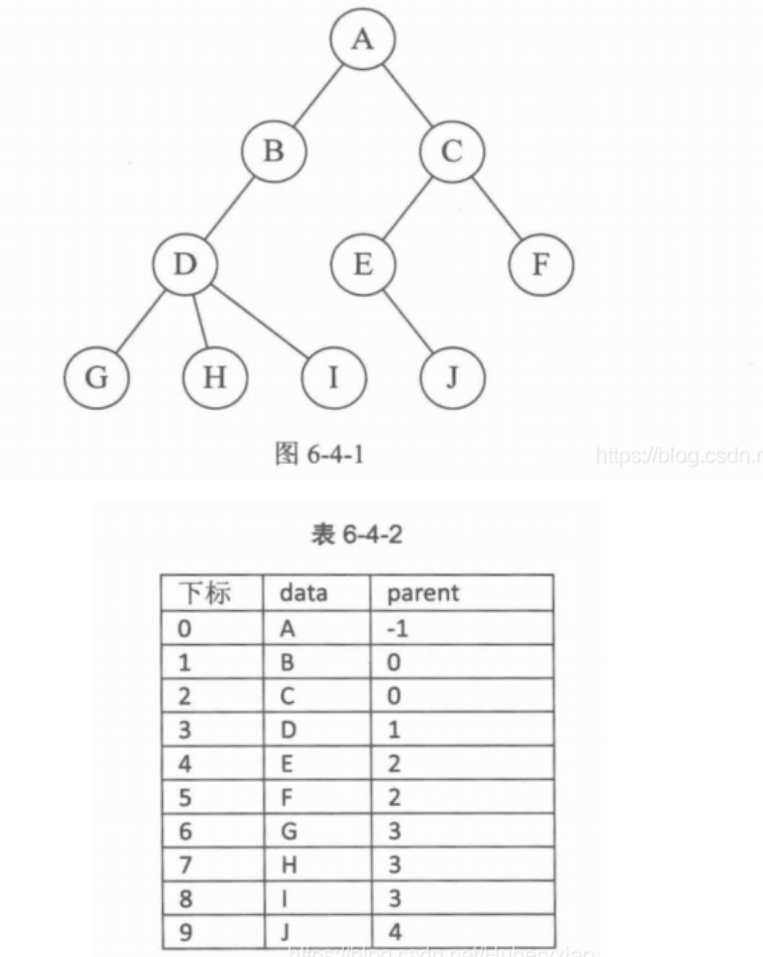
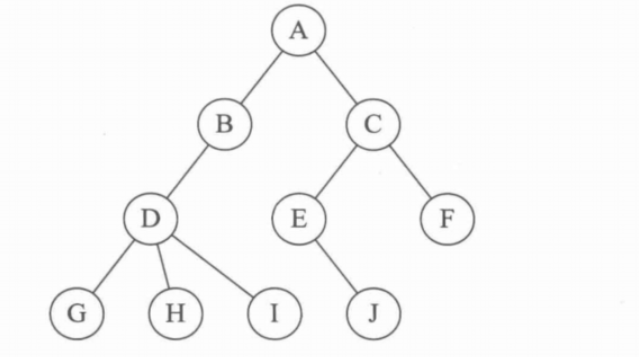
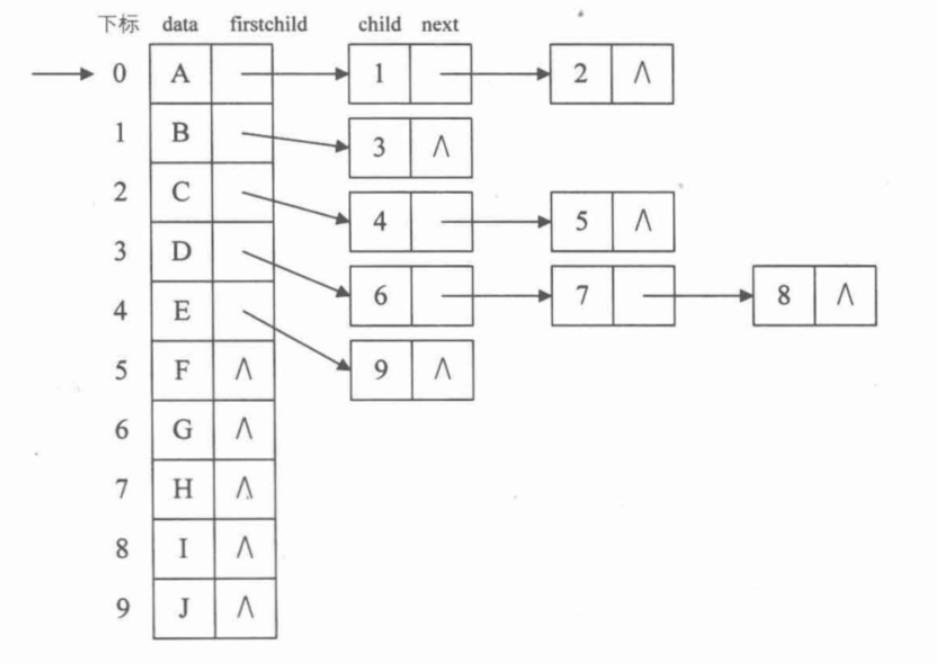
    image_mak

孩子表示法

  • 用数组+链表表示树
    把所有节点放在一个顺序数组中，为每一个节点的孩子们创建一个单链表，遍历该节点的所有孩子。
    image_mak
    image_mak

哈夫曼树

  • 路径：从树中一个结点到另一个结点之间的分支构成这两个结点间的路径

  • 结点的路径长度：两结点之间路径上的分支数

  • 树的路径长度：从树根到每一个结点的路径长度之和．记作：ＴＬ

  • 权（weight)：将树中结点赋给一个有着某种含义的数值，则这个数值为该结点的权

  • 结点的带权路径长度：从根结点到该结点之间的路径长度与该结点的权的乘积．

  • 树的带权路径长度：树中所有叶子结点的带权路径长度之和．记作:WPL(Weighted Path Length)
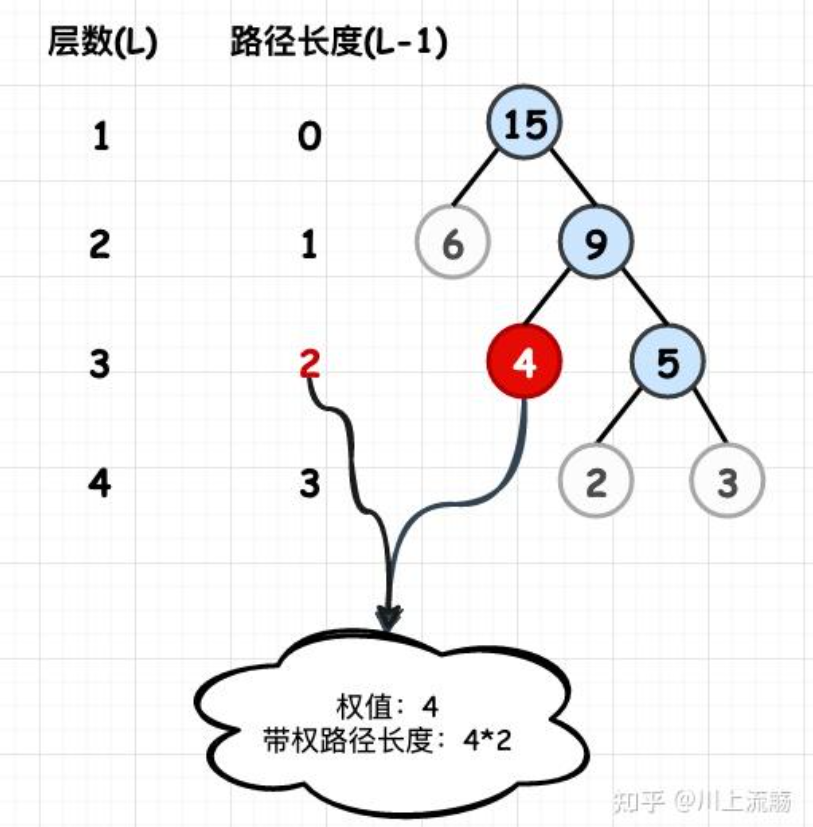
    image_mak
    上图中，WPL = (2+3) * 3 + 4 * 2 + 6 * 1 = 29

  • 定义：最优二叉树，是一类带权路径长度最短的树
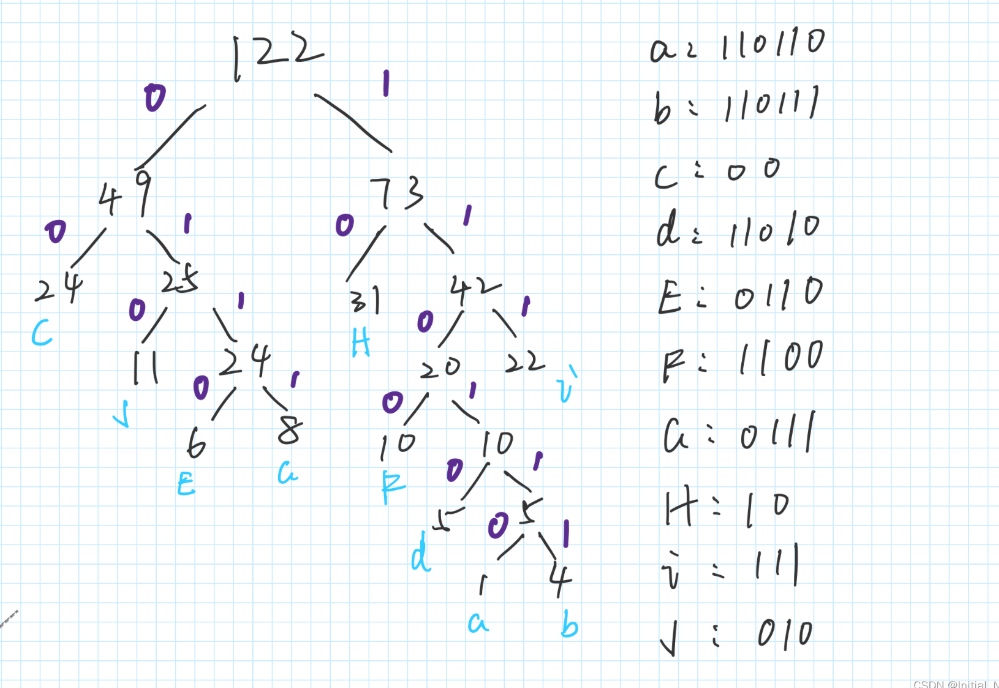
    从权值数组构造：每一轮都将权值最小的作为左右结点归并成一个二叉树，然后把和值加入到序列中，循环直到只剩一个

    • 如:以w(1，4，24，5，6，10，8，31，22，11)构造哈夫曼树:
      image_mak

  • 哈夫曼编码:每个节点左子树边为0,右边为1,一个节点的哈夫曼编码就是从根节点扫下来的读到的序列
    image_mak

图

  • 连通:在无向图中，若从顶点v到顶点w有路径存在，则称v和w是连通的。
  • 连通图:若图G中任意两个顶点都是连通的，则称图G为连通图
  • 强连通:在有向图中，若从顶点v到顶点w和从顶点w到项点v之间都有路径,则称这两个顶点是强连通的。若图中任何一对顶点都是强连通的，则称此图为强连通图。

image_mak

最小生成树

  • 生成树定义:对一个具有 n 个点的连通图进行遍历，对于遍历后的子图，其包含原图中所有的点且保持图连通，最后的结构一定是一个具有 n-1 条边的树，通常称为生成树。

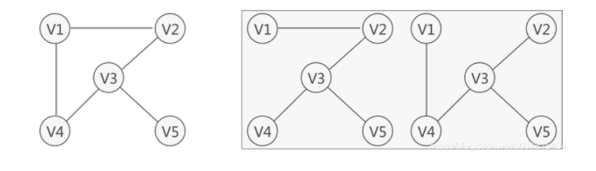
image_mak

  • 最小生成树: n-1 条边的边权之和是所有方案中最小

prim算法:

先随便往集合里加一个点,然后每次都找距离集合里任意一点距离最短的点加入,直到全部连接,见例子:
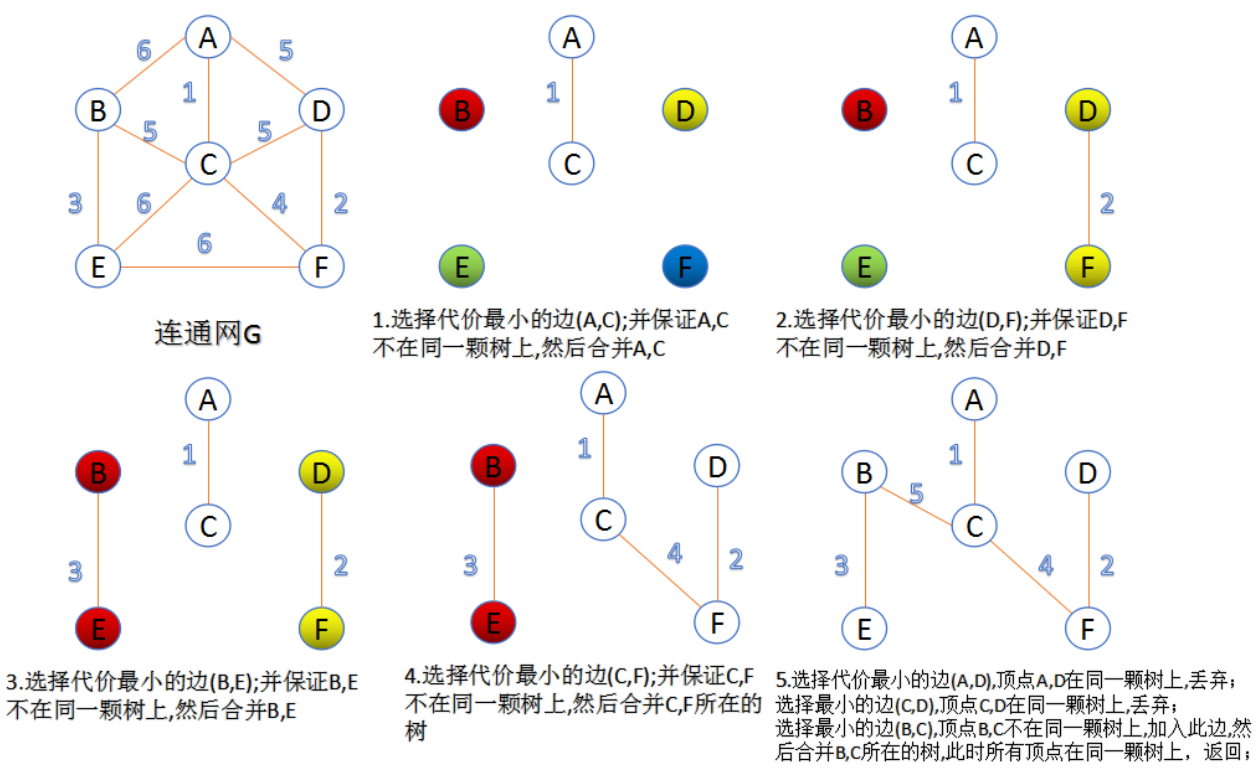
image_mak
image_mak

kruscal算法：

每迭代一次就选择一条不在当前树的最小代价边，加入到最小生成树的边集合里。
image_mak

图的表示方法

邻接矩阵

无向图：
image_mak
有向图：index指向columns
image_mak

邻接表

先以数组存储，然后每个点的指针指向下一个点的下表
无向图：
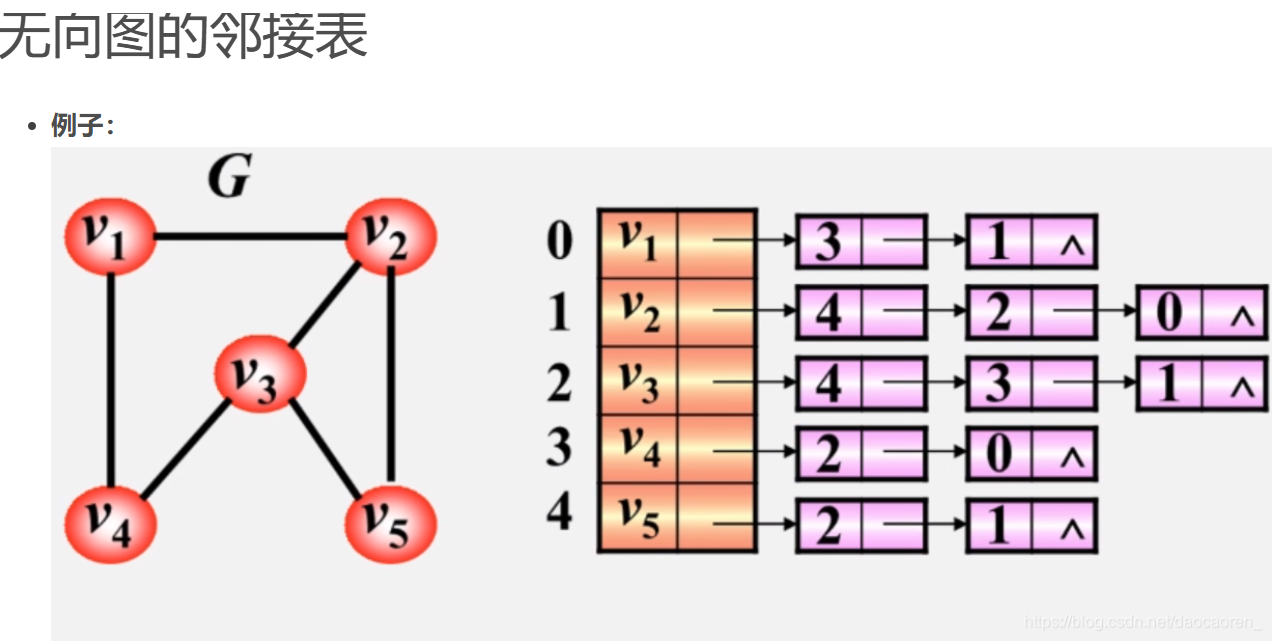
image_mak
有向图：
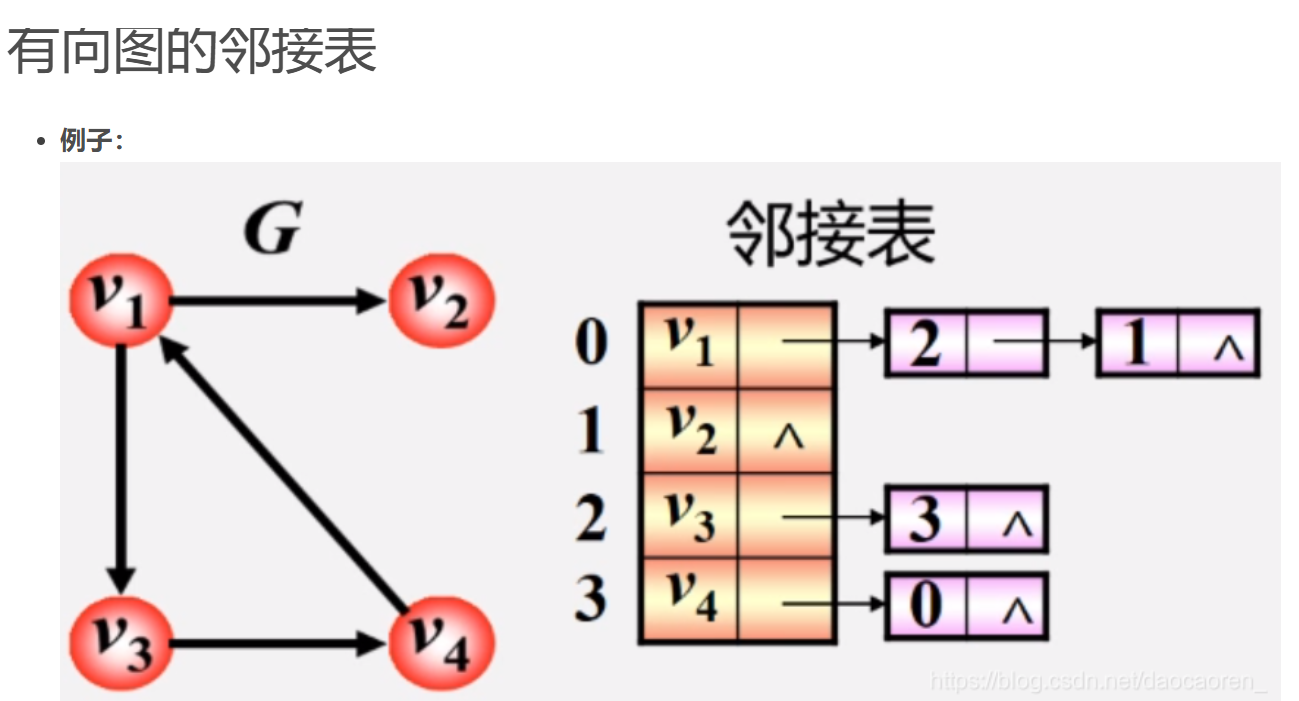
image_mak

图的遍历

深度优先：

  • 从当前节点出发，选择一个尚未访问过的相邻节点进行访问。
  • 如果有多个未访问的相邻节点，随便选
  • 如果当前节点的所有相邻节点都已经被访问过，或者没有未访问的相邻节点，算法会回溯到上一个节点，继续寻找其他未访问的相邻节点。
    • 类比为走迷宫时尽可能沿着一个方向走到底，然后再回溯寻找未探索的路径。
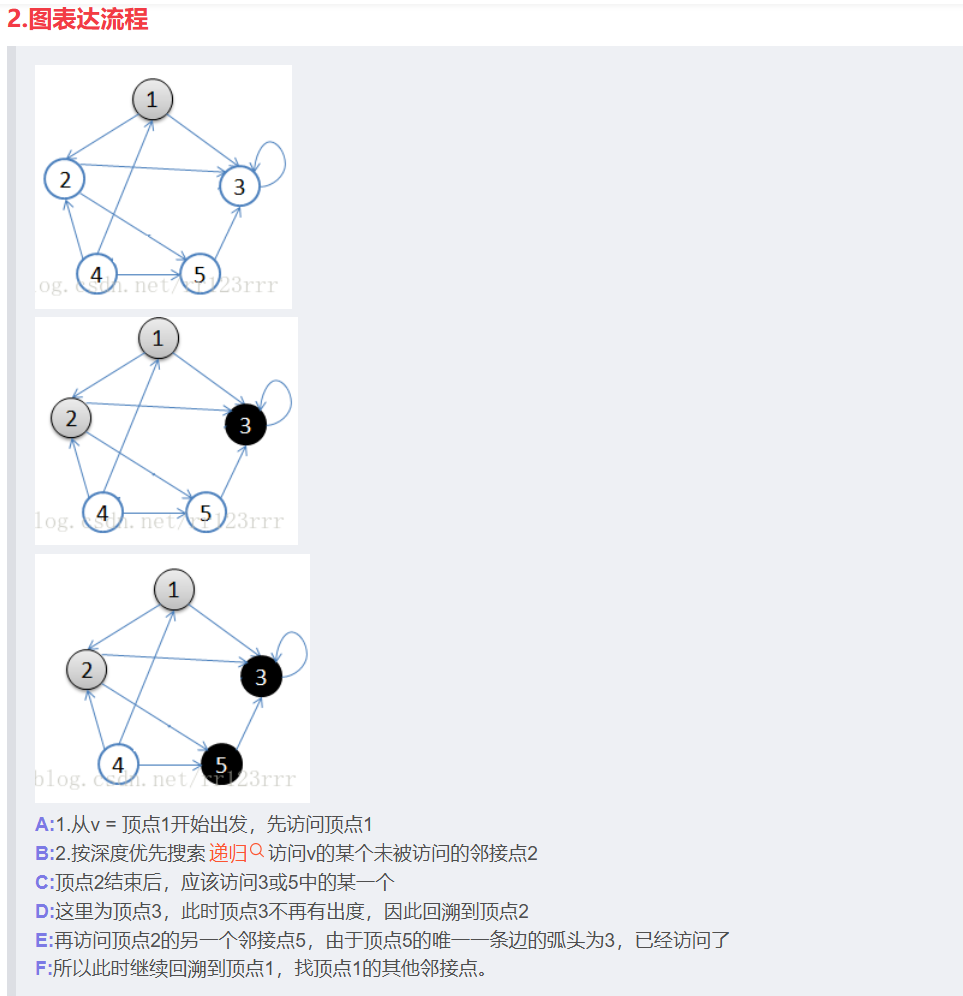
      image_mak

然后发现1没有邻接点，再选一个没有访问过的点，为唯一一个4，所以遍历序列为：

1 → 2 → 3 → 5 → 4

广度优先

以队列形式访问，把每一个节点的所有邻接节点入队，然后从队头出队访问，并把被访问的节点的邻接节点继续入队，以此类推
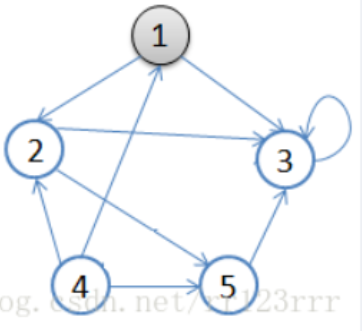
image_mak

起点：节点 1
访问 1 → 标记为已访问。
将相邻节点 2, 3 加入队列。
队列：2, 3

访问节点 2（出队）
访问 2 → 标记为已访问。
将相邻未访问的节点 3, 5 加入队列。
队列：3, 3, 5

访问节点 3（出队）
访问 3 → 标记为已访问。
节点 3 的相邻节点是 3（自环，已访问），忽略。
队列：3, 5

访问节点 3（出队，再次访问，不重复标记）
忽略（已访问过）。
队列：5

访问节点 5（出队）
访问 5 → 标记为已访问。
将相邻未访问节点 3 加入队列（已访问，忽略）。
队列：空

检查未访问节点

未访问的节点还有 4，将其作为新起点。
队列：4
访问节点 4（出队）
访问 4 → 标记为已访问。

将相邻节点 1, 2, 5 加入队列（均已访问，忽略）。

队列：空

最终序列：1 → 2 → 3 → 5 → 4

最短路径

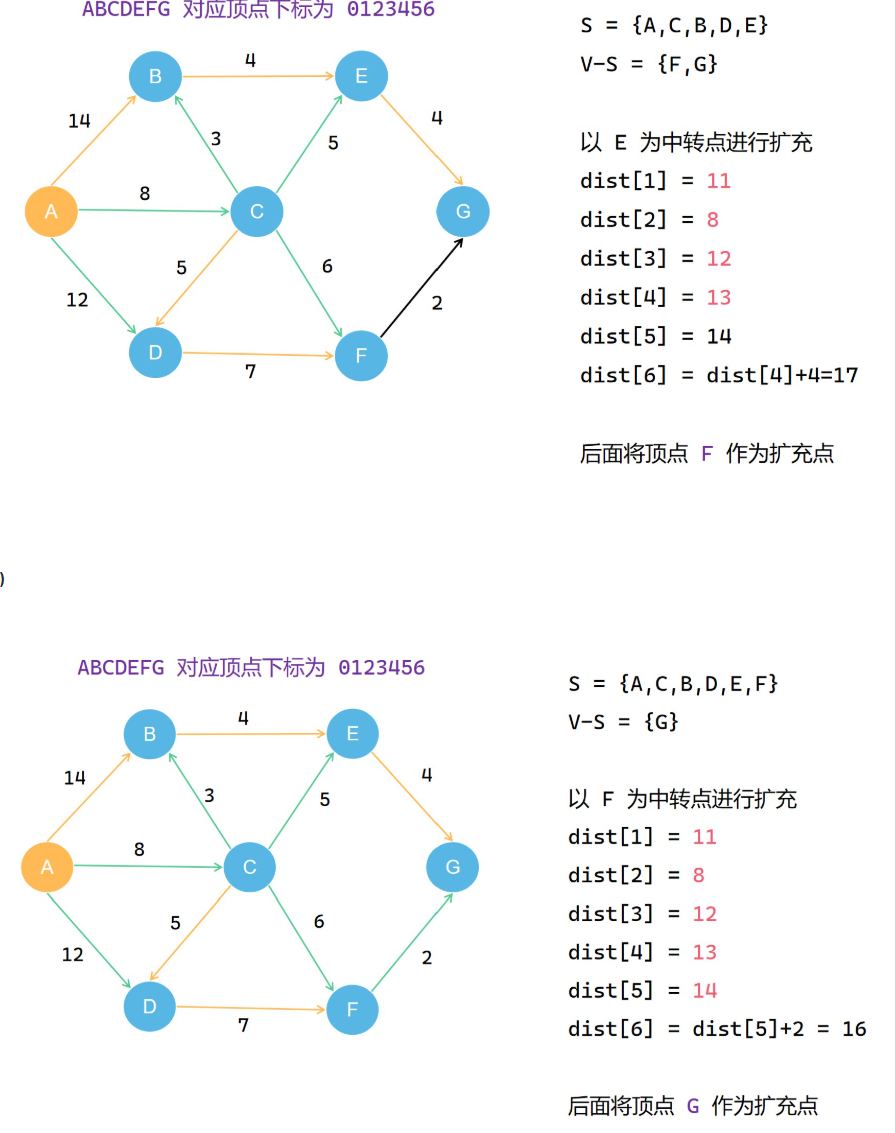
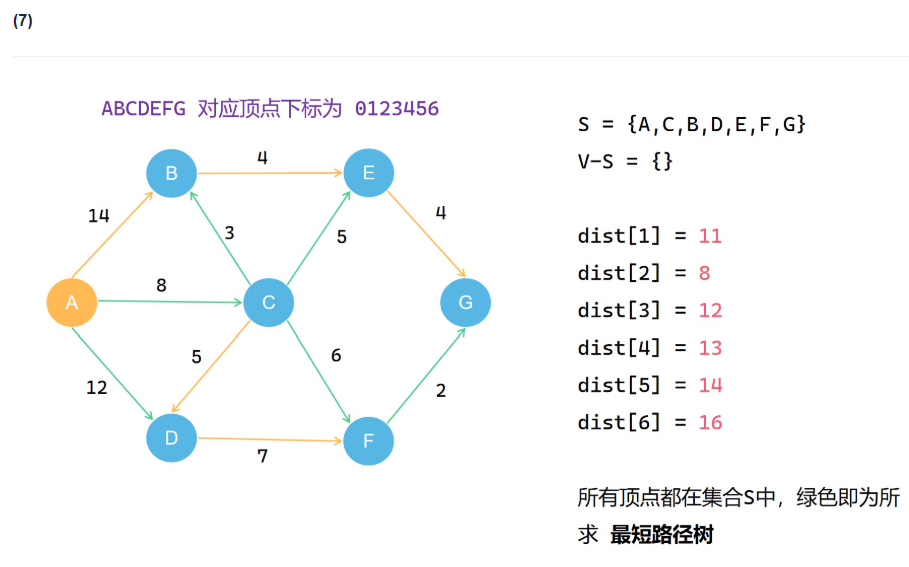
Dijkstra算法

类比prim算法，但是要把过程中得到的每一个路径值存下来
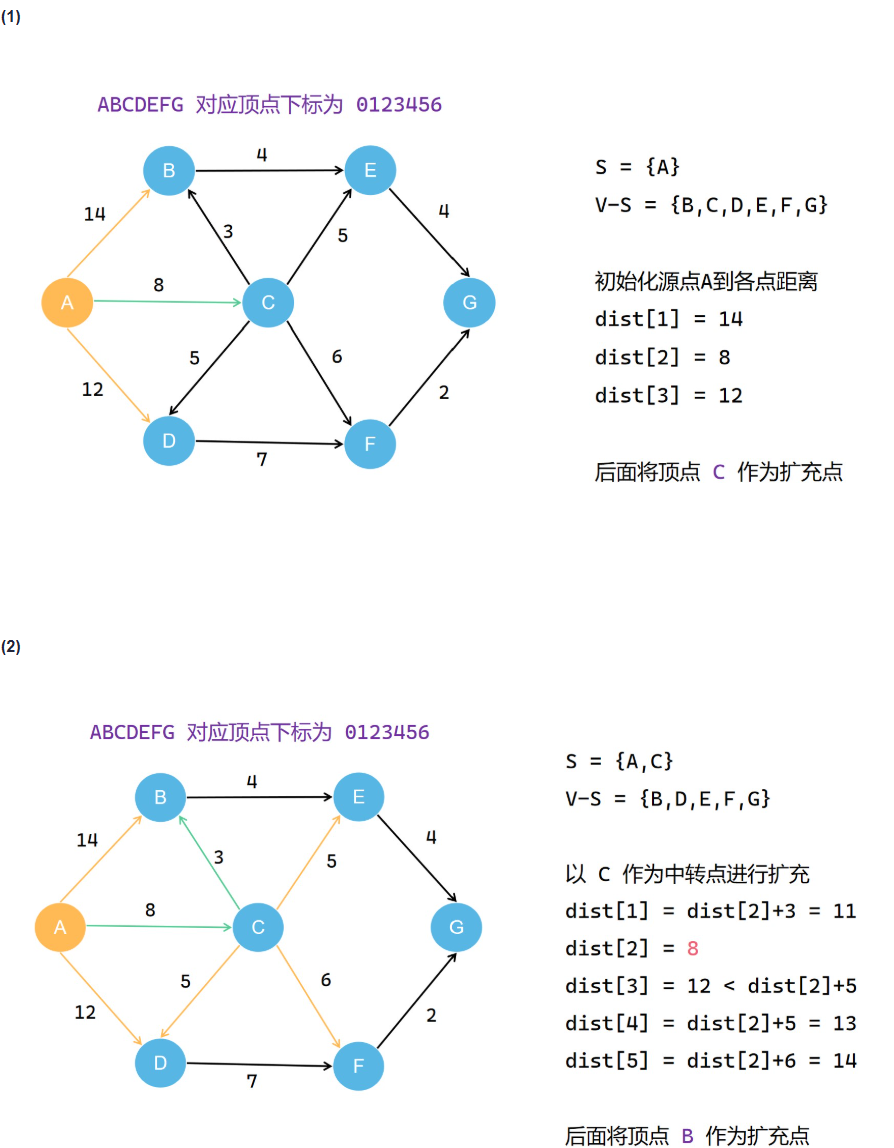
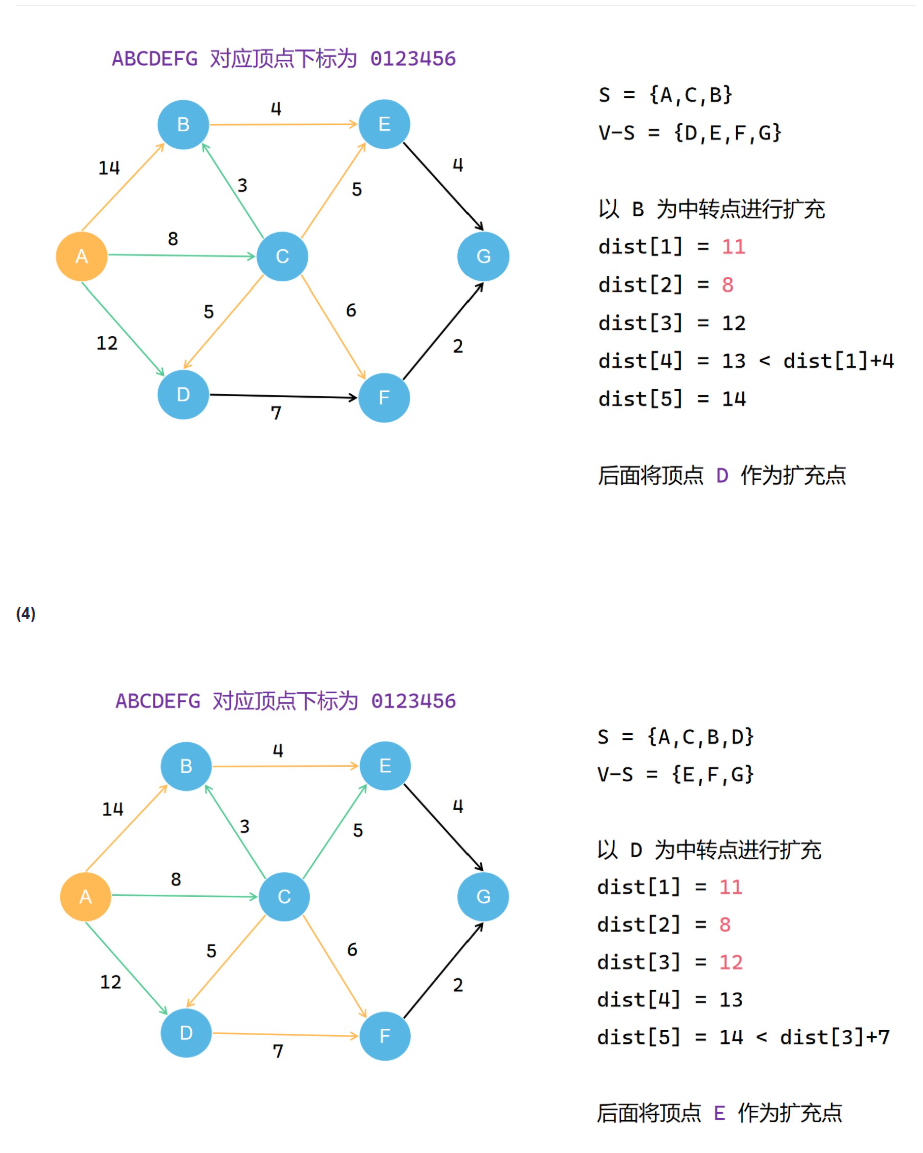
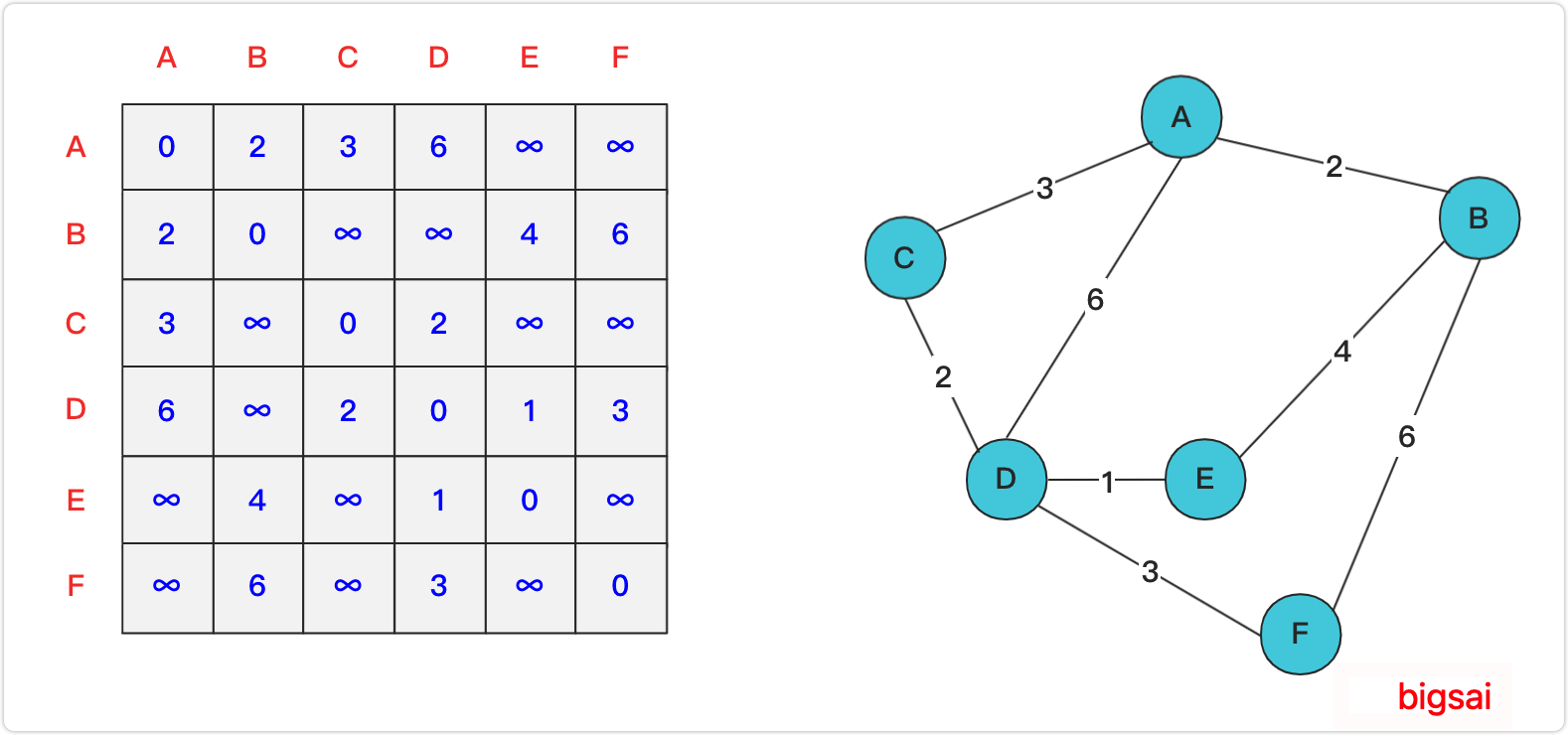
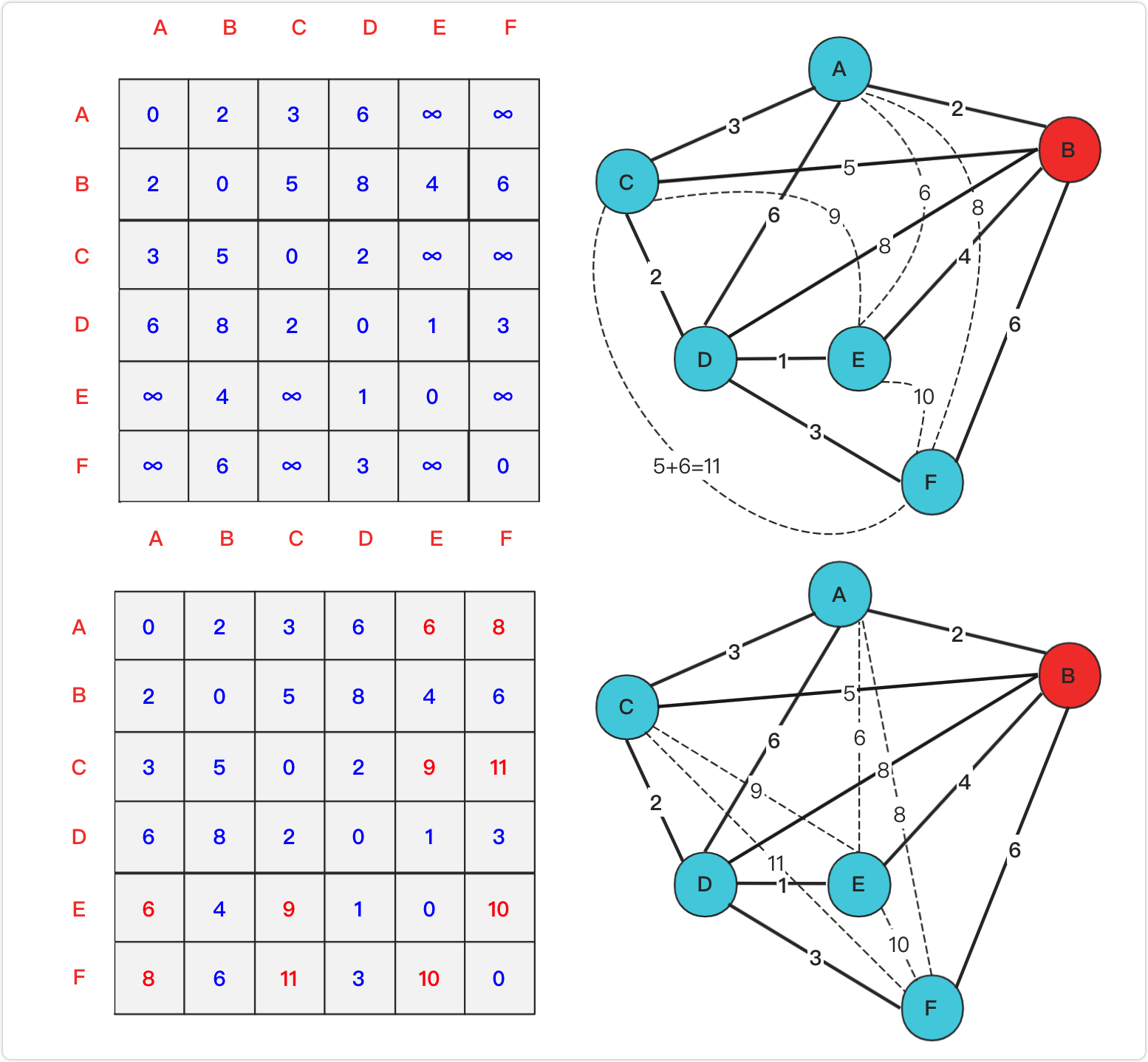
image_mak
image_mak
image_mak
image_mak

Floyd算法

构造矩阵，依次将节点作为中介加入矩阵，并重新计算受中介点影响的各个点之间的距离，将最短的距离更新到表中
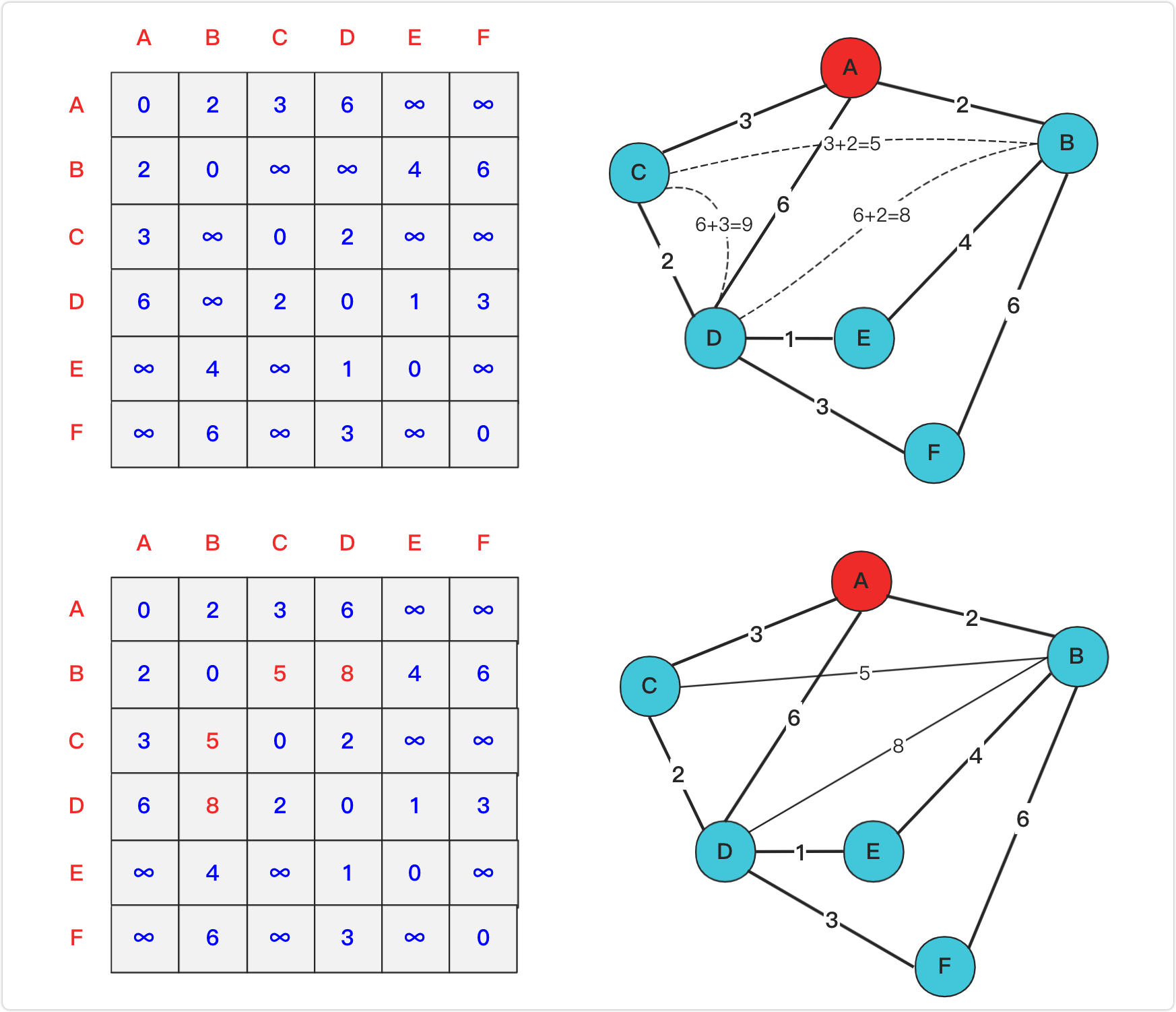
image_mak
加入A为中介后：
image_mak
以此类推，得到：
image_mak

AOV网 AOE网

  • 在有向图中若以顶点表示活动，有向边表示活动之间的先后关系，这样的图简称为AOV网。
  • 在带权有向图中若以顶点表示事件，有向边表示活动，边上的权值表示该活动持续的时间，这样的图简称为AOE网。

查找

哨兵顺序查找

  • ASL：
    • 成功：(n+1)/2
    • 失败：n
  • 遍历时只用进行1次判断
int sentrySearch(int[] arr, int target) {
    if (target == arr[0]) {
        return 0;
    }

    // 将第一个元素保存
    int temp = arr[0];
    // 将目标值放到0号下标出作为哨兵
    arr[0] = target;

    int index = arr.length - 1;
    while (arr[index] != target) {
        --index;
    }

    // 查找完毕，将0号下标元素还原
    arr[0] = temp;

    return index > 0 ? index : -1;
}

折半查找

  • ASL:
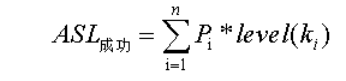
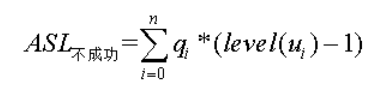
    image_mak
    image_mak
int BSearch(int arr[],int length,int key){
    int left = 0;
    int right = length-1;
    int mid;
    while (left <= right)
    {
        mid = (left + right) / 2;
        if(key == arr[mid]){
            return mid;
        }else if (key < arr[mid])
        {
            right = mid-1;
        }else{
            left = mid +1;
        }        
    }
    return -1;
}

分块查找

// 数据升序排序，分三块
#include <stdio.h>
struct index /*定义块的结构*/
{
    int key;
    int start;
    int end;
} index_table[4]; /*定义结构体数组*/
int block_search(int key, int a[]) /*自定义实现分块查找*/
{
    int i, j;
    i = 1;
    while (i <= 3 && key > index_table[i].key) /*确定在哪个块中*/
        i++;
    if (i > 3) /*大于分得的块数，则返回0*/
        return 0;
    j = index_table[i].start; /*j等于块范围的起始值*/
    while (j <= index_table[i].end && a[j] != key) /*在确定的块内进行查找*/
        j++;
    if (j > index_table[i].end) /*如果大于块范围的结束值，则说明没有要查找的数,j置0*/
        j = 0;
    return j;
}
int main()
{
    int i, j = 0, k, key, a[16];
    printf("please input the number:\n");
    for (i = 1; i < 16; i++)
        scanf("%d", &a[i]); /*输入由小到大的15个数*/
    for (i = 1; i <= 3; i++){
        index_table[i].start = j + 1; /*确定每个块范围的起始值*/
        j = j + 1;
        index_table[i].end = j + 4; /*确定每个块范围的结束值*/
        j = j + 4;
        index_table[i].key = a[j]; /*确定每个块范围中元素的最大值*/
    }
    printf("please input the number which do you want to search:\n");
    scanf("%d", &key); /*输入要查询的数值*/
    k = block_search(key, a); /*调用函数进行查找*/
    if (k != 0)
        printf("success.the position is :%d\n", k); /*如果找到该数，则输出其位置*/
    else
        printf("not found!"); /*若未找到则输出提示信息*/
}

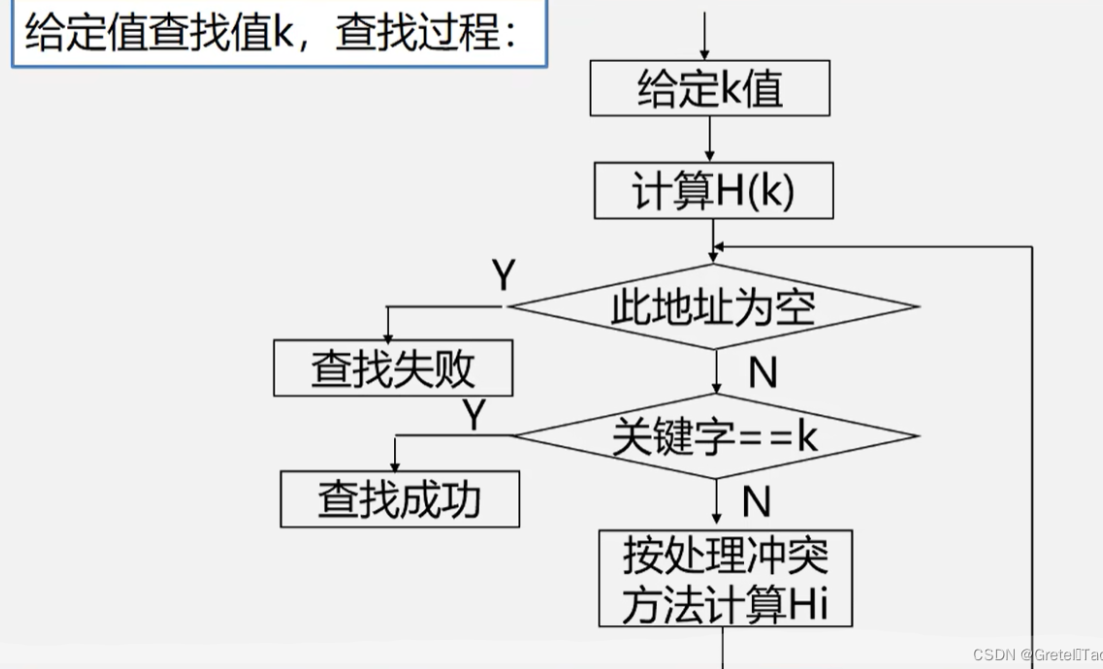
散列表查找

  • 散列表：计算每个元素的hash来映射
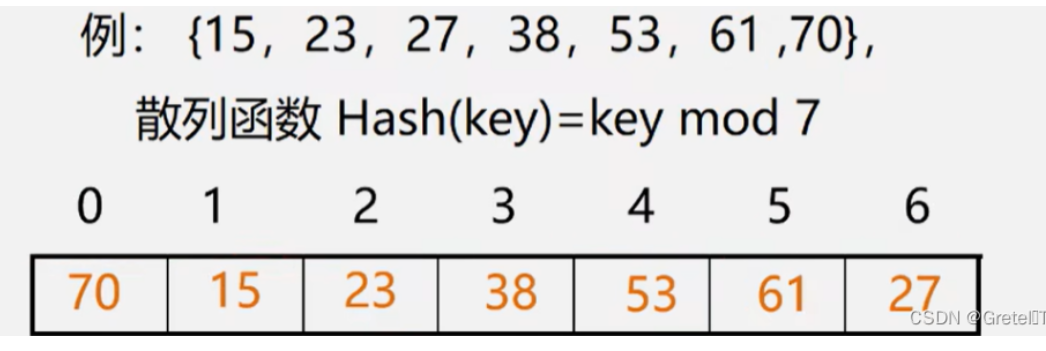
    image_mak
    当hash(a)=hash(b)的时候就要处理冲突
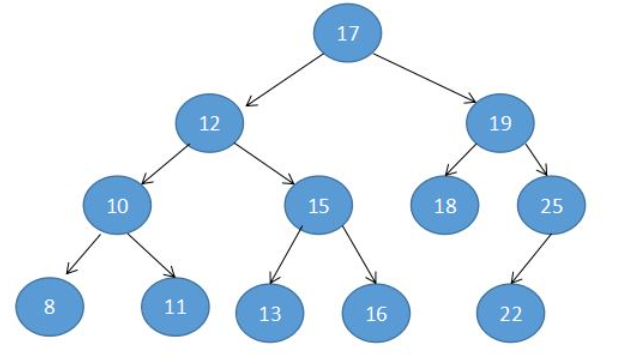
    image_mak
    image_mak
    image_mak

排序

image_mak

二叉排序树

左 < 根 < 右
image_mak

冒泡排序

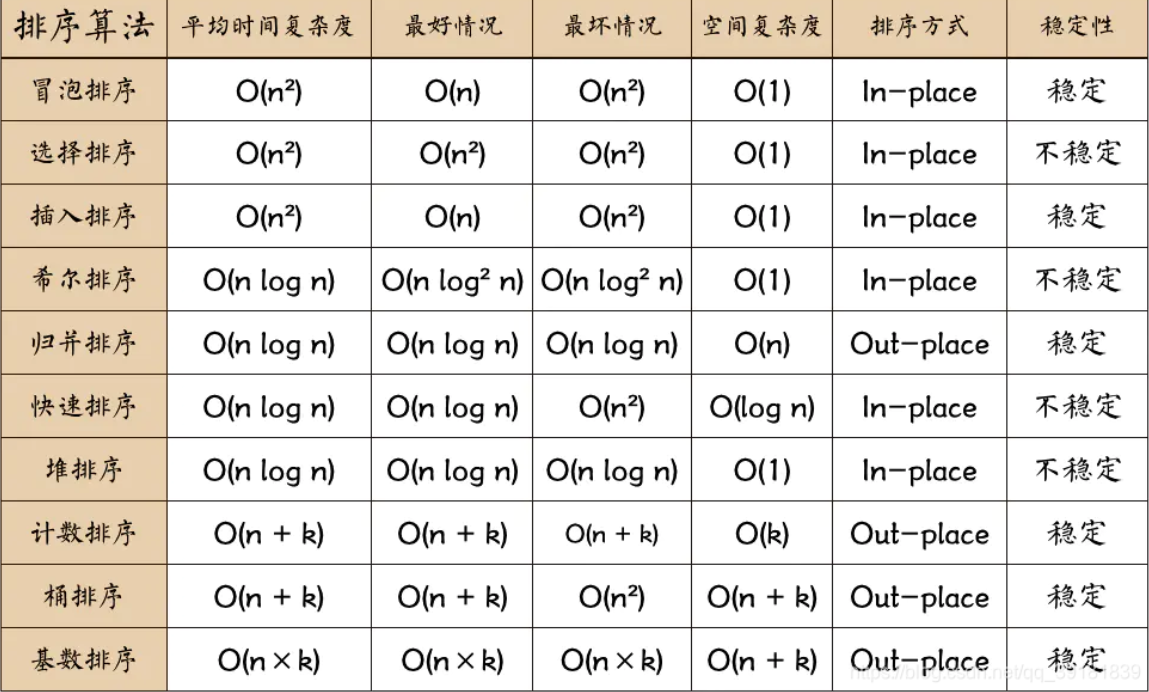
  • 时间复杂度：O( n^2 )；
  • 空间复杂度：最差O(n)；平均O(1)；最好n
void bubble_sort(int arr[], int len) {
        int i, j, temp;
        for (i = 0; i < len - 1; i++)
                for (j = 0; j < len - 1 - i; j++)
                        if (arr[j] > arr[j + 1]) {
                                temp = arr[j];
                                arr[j] = arr[j + 1];
                                arr[j + 1] = temp;
                        }
}

选择排序

  • 时间复杂度:O(N ^2)
  • 空间复杂度:O(1)
void swap(int *a,int *b) //交換兩個變數
{
    int temp = *a;
    *a = *b;
    *b = temp;
}
void selection_sort(int arr[], int len)
{
    int i,j;

        for (i = 0 ; i < len - 1 ; i++)
    {
                int min = i;
                for (j = i + 1; j < len; j++)     //走訪未排序的元素
                        if (arr[j] < arr[min])    //找到目前最小值
                                min = j;    //紀錄最小值
                swap(&arr[min], &arr[i]);    //做交換
        }
}

插入排序

  • 时间复杂度：O(n^2);最好的情况：O(n)
  • 空间复杂度：O(1)
void insertion_sort(int arr[], int len){
        int i,j,key;
        for (i=1;i<len;i++){
                key = arr[i];
                j=i-1;
                while((j>=0) && (arr[j]>key)) {
                        arr[j+1] = arr[j];
                        j--;
                }
                arr[j+1] = key;
        }
}

堆排序

  • 升序用大根堆，降序用小根堆
  • 时间复杂度：O(n log n)，空间复杂度：O(1)

交换堆顶元素和末尾元素：将堆顶元素（最大值）与末尾元素交换，并将堆的大小减一。
调整堆：对堆顶元素进行调整，使其满足最大堆性质。
重复直到堆的大小为1

// 调整堆，使其满足最大堆性质
void heapify(vector<int>& arr, int n, int i) {
    int largest = i; // 初始化最大值为根节点
    int left = 2 * i + 1; // 左子节点
    int right = 2 * i + 2; // 右子节点

    // 如果左子节点大于根节点
    if (left < n && arr[left] > arr[largest])
        largest = left;

    // 如果右子节点大于最大值
    if (right < n && arr[right] > arr[largest])
        largest = right;

    // 如果最大值不是根节点
    if (largest != i) {
        swap(arr[i], arr[largest]); // 交换根节点和最大值节点
        heapify(arr, n, largest); // 递归调整子树
    }
}

// 构建最大堆
void buildMaxHeap(vector<int>& arr, int n) {
    for (int i = n / 2 - 1; i >= 0; i--)
        heapify(arr, n, i);
}

// 堆排序
void heapSort(vector<int>& arr) {
    int n = arr.size();

    // 构建最大堆
    buildMaxHeap(arr, n);

    // 一个个取出元素
    for (int i = n - 1; i > 0; i--) {
        swap(arr[0], arr[i]); // 将当前最大值移到数组末尾
        heapify(arr, i, 0); // 调整堆
    }
}

快速排序

key取arr[-1]，left从左往右找找到比key大的，使得a[right]=a[left]，然后right开始从右往左找，找到比key小的，使得a[left]=a[right]，然后left又开始往右找，直到left=right完成一次循环。然后把a[left]=key，此时key左边都是比他小，右边都是比他大

void quickSort(int nums[], int start, int end) {
    //数组有多个元素进行排序
    if (start < end) {
        int base = nums[start];//以要进行排序数组第0个元素为base
        int left = start;//左指针
        int right = end;//右指针
        while (left < right) {
            //从右向左找，比base大，right--
            while (left< right && nums[right] >= base) {
                right--;
            }
            //比base小，替换left所在位置的数字
            nums[left] = nums[right];
            //从左向右找，比base小，left++
            while (left < right && nums[left] <= base){
                left++;
            }
            //比base大，替换right所在位置的数字
            nums[right] = nums[left];
        }
        nums[left] = base;//此时left=right，用base替换这个位置的数字
        //排列比base小的数字的数组
        quickSort(nums, start, left - 1);
        //排列比base大的数字的数组
        quickSort(nums, left + 1, end);
    }
}


A web ctfer from 0RAYS
最后更新于 2025-01-08
啥也没有呀